Project 1: A-Maze-ing Stacks and Queues
Overview
In this project you will implement the Stack and Queue interface
using a LinkedList, ArrayList, and a CircularArrayList to both
solve and generate mazes. Amazing! You will do so without using
the java.util library, which means, you'll have to do ALL the
implementation work yourself.
Due Date
This project is due Sunday, October 1nd at 2359
Grading
There are many different parts to the project. Based on how much you complete, the maximum grade is described below:
- Grade: 25%
- Complete the
LinkedListimplementation of a O(n) Queue
- Complete the
- Grade: 45%
- Complete the
LinkedListimplementation of a O(n) Queue - Use
LinkedListimplementation of a Queue to solve the provided mazes
- Complete the
- Grade: 60%
- Complete the
LinkedListimplementation of a O(n) Queue and O(1) Stack - Used
LinkedListimplementation of a Queue to solve the provided mazes
- Complete the
- Grade: 75%
- Complete the
LinkedListimplementation of a O(n) Queue and O(1) Stack - Used
LinkedListimplementation of a Queue to solve the provided mazes - Used
LinkedListimplementation of a Stack to generate new mazes
- Complete the
- Grade: 80%
- Complete the
LinkedListimplementation of a O(1) Queue and O(1) Stack - Used
LinkedListimplementation of a Queue to solve the provided mazes - Used
LinkedListimplementation of a Stack to generate new mazes
- Complete the
- Grade: 85%
- Complete the
LinkedListimplementation of a O(1) Queue and O(1) Stack - Complete the
ArrayListimplementation of a O(1) amortized Stack - Used
LinkedListimplementation of a Queue to solve the provided mazes - Used
ArrayListimplementation of a Stack to generate new mazes
- Complete the
- Grade: 95%
- Complete the
LinkedListimplementation of a O(1) Queue and O(1) Stack - Complete the
ArrayListimplementation of a O(1) amortized Stack - Complete the
CircularArrayListimplementation of a O(1) amortized Queue - Used
CircularArrayListimplementation of a Queue to solve the provided mazes - Used
ArrayListimplementation of a Stack to generate new mazes
- Complete the
- Grade: 100%
- Complete the
LinkedListimplementation of a O(1) Queue and O(1) Stack - Complete the
ArrayListimplementation of a O(1) amortized Stack - Complete the
CircularArrayListimplementation of a O(1) amortized Queue and O(1) amortized Stack - Used
CircularArrayListimplementation of a Queue to solve the provided mazes - Used
CircularArrayListimplementation of a Stack to generate new mazes
- Complete the
Partial credit and deductions will be provided based on quality of work. For example, we will heavily test your data structures at the extremes, so performance matters! Plus, if you have any \(O(n)\) operations in your stack and queue it will impact the performance of your maze algorithms and be exposed in our testing.
You must fully complete each of the List implementation for full credit. This includes the entire List interface in addition to the appropriate Queue/Stack interface.
Submission and Starter Code
All starter code for this project can be obtained via the
~aviv/bin/ic312-up and submission will occur via
~aviv/bin/ic312-submit.
You must submit the following edited file(s):
ic312/LinkedList.javaic312/ArrayList.javaic312/CircularArrayList.javaSolveMaze.javaDrawMaze.javaREADME: containing any attribution or notes for grading.- Any testing files you'd like us to look at and consider during grading.
Description
Solving and Generating Mazes
You will be asked to solve and generate mazes using a queue and a stack, respectively. These processes are independent of the implementation choices for the queue and stack.
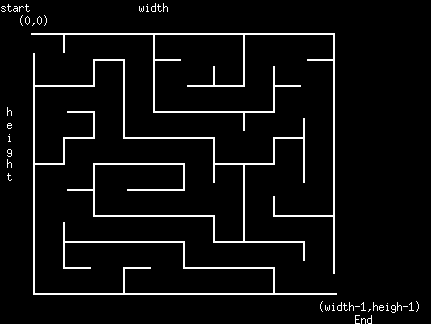
Let's consider a maze as a 2-D array of spaces, where between each
space there is a wall or not. The start point of the maze will be the
upper left and the finish point is the lower right. For example, we
will use the following maze maze0.ser in this example.
Notice that the maze has a width and height, and we index spaces in
the maze with (w,h). The top left index is (0,0), and the bottom
right index is (width-1,height-1). The maze will always start in the
upper left and finish in the bottom right. We will describe two spaces
as "reachable" if they are adjacent and do not have a wall between
them.
Solving a Maze with a Queue
The process of solving a maze with queue is a lot like "hunting" out the end point from the start point. To do that, we must ensure that we test all possible paths. The queue will allow us to track which spaces we should visit next.
The basic routine works as follows:
- Initialize a queue with the start index (0,0)
- Loop Until: queue is empty
- Dequeue current index and mark it as visited
- If current index is the finish point
- Break! We've found the end
- Enqueue all indexes for reachable and unvisited neighbors of the current index
- Continue the loop.
Looking over this routine, imagine the queue, full of maze-spaces. Each time you dequeue a maze-space you are searching around for more spaces surrounding that space to search around next. If you find any, you add them to the queue to eventually be analyzed later. This repeats until you find the end of the maze.
Because of the FIFO nature of a queue, the resulting search pattern is a lot like a water rushing out from the start space, through all possible path in the maze until the end is reached. This search pattern is also referred to as Breadth First Search (or BFS).
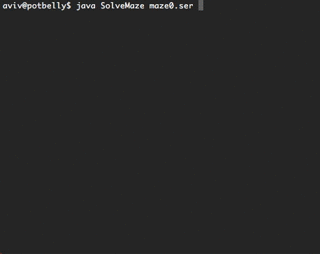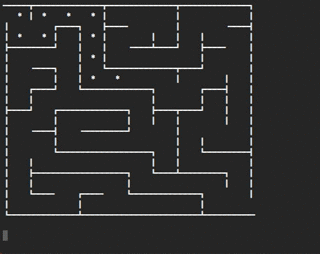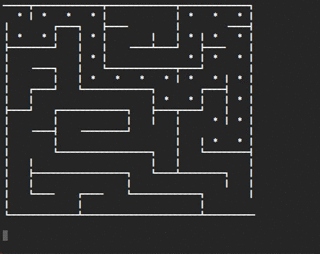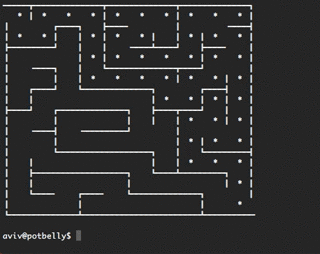
Here's a gif of what the solving routine will look like. The * shows
a space being visited.
IMPORTANT! For consistency, you should always enqueue the indexes
into the queue in the order that they are provided via the
getReachableUnvisited() neighbors method (see below). That is
enqueue index 0 of the returned list first, then the next index, and
so on. In this way, your algorithm will match mine and should work
like the animation above. The final state of your maze should look
like below:
Drawing a Maze with a Stack
The process of drawing a maze is very similar to solving a maze, but instead the goal is to explore all spaces, removing walls along the way, such that there exist a path between any two spaces through a series of reachable spaces. That also means that there will exist a path from the from the start to the end.
The algorithm to ensure all reachability will work as follows:
- Initialize a stack with the start index (0,0)
- Loop Until: stack is empty
- pop current index off the stack and mark it as visited
- If current index has any unvisited neighbors
- Choose a random unvisited neighbor index
- Remove the wall between the chosen neighbor index and the current index
- push the current index on the stack
- push the randomly choose neighbor index on the stack
- Continue the loop.
Looking over this routine, you should be able to invision how this procedure will dive through the maze randomly, like a snake, until the snake reaches a dead end (a space without any unlisted neighbors). The exploration of the snake would then have to backtrack until there is a space with unvisited neighbors and explore from there. Eventually, the snake will have explored the entire maze, at which point, you're done. This search pattern is also referred to as Depth First Search (or DFS)
Here's a gif of what the maze drawing routine would look like. The *
shows a space being visited.
For consistency, you should make a random choice from the reachable neighbors like so:
int r = rnd.nextInt(l.size());
Where l is the list of reachable neighbors, rnd is a Random
object, and r is the index of the randomly selected neighbor. If you
follow this procedure, you should be able to match the generation
routine in the above animation.
The seed for this random object will be specified on the command line, like below. This means, for a given width, height, and seed, you should always generate the same maze.
Maze files
You are provided with three sample maze files, maze0.ser,
maze1.ser, and maze2.ser. The *.ser extension stands for
"serialized" because each file is just serialization of a Maze
object.
The maze files will serve two purposes for you: (1) it will provide you sample mazes to solve while you are unable to test your maze drawer, and (2) it will provide something to test against for your maze drawer. Each of the files were generated with the following commands:
java DrawMaze maze0.ser 10 10 10java DrawMaze maze1.ser 10 20 30java DrawMaze maze2.ser 25 25 25
To print the mazes, you can use the provided PrintMaze.java program.
Maze.java and Space.java
To facilitate your programming, all the basic maze functionality is
provided to you in two java files: Maze.java and Space.java. You
may look over that code (there are comments) but do not edit those files.
Here are some relevant methods you will need to call in your code.
/* Maze class methods*/
//return a List of index pairs of all the unvisited neighbors of the index (h,w)
public List<Pair<Integer,Integer>> getUnvistedNeighbors(int h, int w)
//return a List of index pairs of all the unvisited and reachable
//neighbors (no walls between) of the index (h,w)
public List<Pair<Integer,Integer>> getReachableUnvistedNeighbors(int h, int w)
//remove a wall from index (h,w) at the directions
//Space.LEFT, Space.RIGHT, Space.UP, Space.DOWN
public void removeWall(int h, int w, int direction)
//mark index (h,w) visited
public void visit(int h, int w)
//check if a index (h,w) is visited
public boolean isVisited(int h, int w)
The ic312 package
You are not allowed to use java.util for this project, and instead,
you will be building up and using the ic312 package of data
structures. This package is imported in all the provided Java files:
import ic312.*.
In the package directory you will find the following classes definitions. Of those, you you should not edit (but feel free to use and read over):
List.java: Definition of the List interfaceQueue.java: Definition of the Queue interfaceStack.java: Definition of the Stack interfacePair.java: A pair class for storing pairs of genericly defined objects (potentially of different types)
You will be required to edit the following files
LinkedList.java: A recursive Linked List implementation that implements the List, Queue, and Stack interfaces. You will need to complete the interface implementations for Stack and Queue and make sure it is O(1) in Stack/Queue operations (this will require adding a tail pointer and perhaps editing other aspects of the file HINT).ArrayList.java: A array based List implementation that implements List and Stack. It is interface implementation is incomplete for all interfaces, and you should complete it.CircularArrayList.java: A circular array based implementation of a List that can implements a Stack and Queue. It is interface implementation is incomplete for all interfaces, and you should complete it.
As all of these items are part of a package, you should compile and use them outside of the package directory. What this means, is that, for example, to compile the LinkedList.java file after you edit it, you do so outside the package directory, like so:
aviv@potbelly:sol$ javac ic312/LinkedList.java
If you were to do so within the package directory, you'll get an error that it can't find the interfaces.
aviv@potbelly:sol$ cd ic312/
aviv@potbelly:ic312$ javac LinkedList.java
LinkedList.java:4: error: cannot find symbol
public class LinkedList<T> implements List<T>,Queue<T>,Stack<T>{
^
symbol: class List
LinkedList.java:4: error: cannot find symbol
public class LinkedList<T> implements List<T>,Queue<T>,Stack<T>{
^
symbol: class Queue
LinkedList.java:4: error: cannot find symbol
public class LinkedList<T> implements List<T>,Queue<T>,Stack<T>{
^
symbol: class Stack
3 errors
The reason for this is that the package lookup procedures is path dependent. I agree this is a bit awkward and non-ideal, but this is the way it is.
Hints and Tips
If you've read this far, congratulations! You've won a nice reward of some hints and tips for completing this project.
- Work in small pieces with achievable goals. There may seem like a lot to do, but many of the parts can be broken down into smaller tasks.
- Test your List implementations separately from your Maze solver/drawer. Testing two different algorithms at once can get complicated.
- The Linked List you are provided is the same from the HW3, but that also means it is not our best implementation. Be sure to ensure that the operations that can be O(1) are, such as size().
- Once you have a working Linked List implementation for stacks and queus, you can complete the entire Maze solver/drawer routines, which leaves you only to deal with the Array List implementations.
- The Array List is very much like the Fixed List from HW1, but with expansion. It shouldn't be too hard to take that version of the code and adapt it to your needs.
When working with generic, remember that you have to indicate the generic type for both deceleration and instantiation.
List<Integer> l = new LinkedList<Integer>(); //generics at declearatoin and instantiation- Ask questions early and often! We are here to help you, but we can't do that if we don't know you need it.