HW 9: Graphs
Solution
Consider the Adjacency list representation of a graph below:
A: [(A, C, 6), (A, G, 5)] B: [(B, C, 7), (B, D, 8), (B, G, 5)] C: [(C, A, 6), (C, B, 7), (C, E, 3), (C, F, 7), (C, G, 3), (C, H, 9)] D: [(D, B, 8), (D, H, 8)] E: [(E, C, 3), (E, F, 4)] F: [(F, E, 4), (F, C, 7)] G: [(G, A, 5), (G, B, 5), (G, C, 3)] H: [(H, C, 9), (H, D, 8)]
[10 points] Describe the important properties of the graph above, using the terminology we know about graphs. (Is it directed/undirected, cyclic/acyclic, connected/unconnected, etc.)
This graph has 8 vertices and 11 edges. It is undirected, weighted, connected, and cyclic. Since the largest possible number of edges for an undirected graph with 8 vertices would be 28, this graph is also fairly sparse.
[15 points] Draw a picture of the graph above.

[20 points] Show the adjacency matrix representation of the graph above.
A B C D E F G H A - - 6 - - - 5 - B - - 7 8 - - 5 - C 6 - - - 7 - 3 9 D - 8 - - - - - 8 E - - 3 - - 4 - - F - - 7 - 4 - - - G 5 5 3 - - - - - H - - 9 8 - - - -
[20 points] Perform a depth-first traversal of the graph above, starting with node A at the top of the stack, and list the order the nodes are visited in. Show your work.
The top of the stack is to the left and we push in order of the adjacency list
Stack: A <-top Visited: Stack: C G <-top Visited: A Stack: C A B C <-top Visited: A G Stack: C A B A B E F G H <-top Visited: A G C Stack: C A B A B E F G C D<-top Visited: A G C H Stack: C A B A B E F G C B H <-top Visited: A G C H D (already visited H) Stack: C A B A B E F G C B <-top Visited: A G C H D Stack: C A B A B E F G C C D G<-top Visited: A G C H D B (already visited G, C and D) Stack: C A B A B E F <-top Visited: A G C H D B Stack: C A B A B E E C <-top Visited: A G C H D B F (already visited C) Stack: C A B A B E E <-top Visited: A G C H D B F Stack: C A B A B E <-top Visited: A G C H D B F E DONE! DFS: A G C H D B F E
[20 points] Perform a breadth-first traversal of the graph above, starting at node A, and list the order the nodes are visited in. Show your work.
The head of queue is to the left
Queue: A Visited: Queue: C G Visited: A Queue: G A B E F G H Visited: A C Queue: A B E F G H A B C Visited: A C G (already visited A) Queue: B E F G H A B C Visited: A C G Queue: E F G H A B C C D G Visited: A C G B Queue: F G H A B C C D G C F Visited: A C G B E Queue: G H A B C C D G C F E C Visited: A C G B E F (already visited G) Queue: H A B C C D G C F E C Visited: A C G B E F Queue: A B C C D G C F E C C D Visited: A C G B E F H (already visisted A,B, and C) Queue: D G C F E C C D Visited: A C G B E F H Queue: G C F E C C D B H Visited: A C G B E F H D DONE! BFS: A C G B E F H D
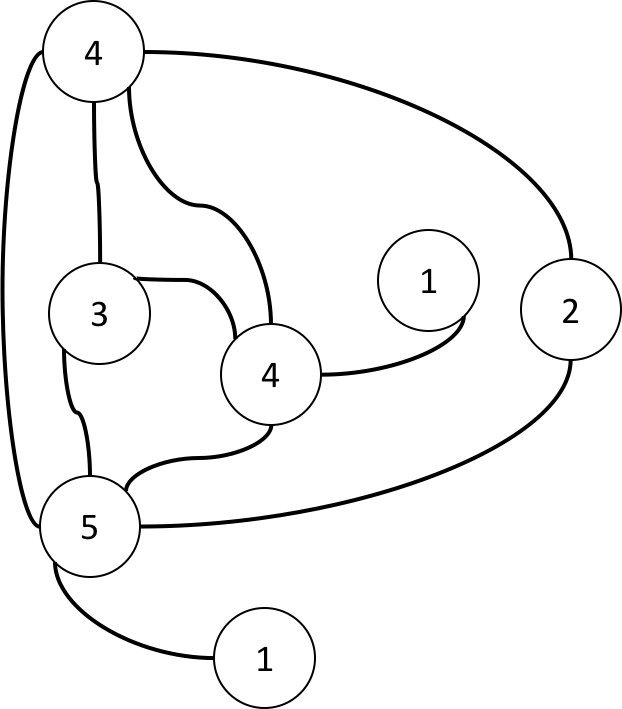
[15 points] Draw an undirected, unweighted graph with 7 vertices, and the following degrees of each vertex: \[2, 3, 1, 4, 4, 5, 1\] Label each vertex with its degree in your final, neatly drawn graph.