1. Draw the following tree after a left rotation at the node 25.

   

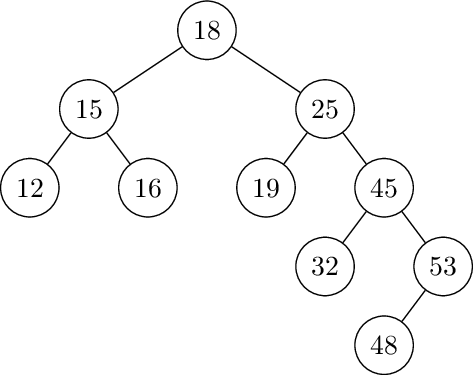
   Solution:

   

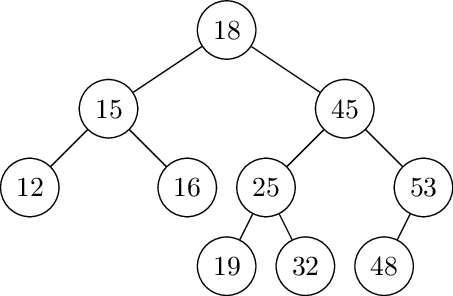
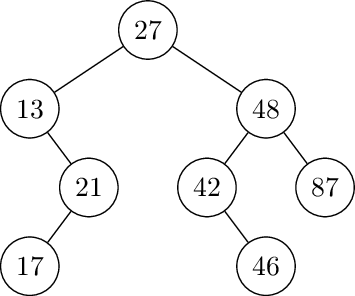
2. Copy the following tree and write the balance factor of each of the nodes. If there is any node out of balance, perform the rotation(s) that will create an AVL tree. You must show the tree after each rotation if there are multiple rotations.

   

   Solution with balance factors:

   

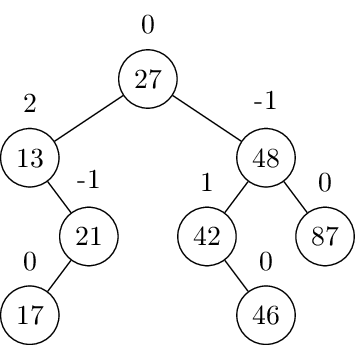
   13 is out of balance, requiring a double rotation. First left rotate at 21:

   

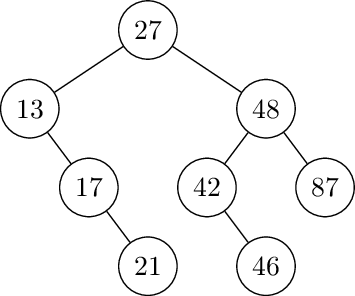
   Then right rotate at 13:

   

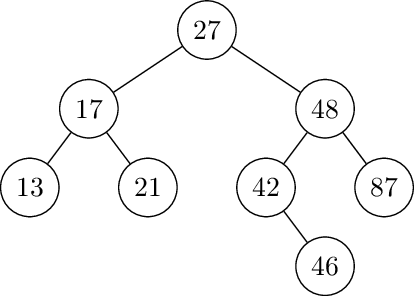
For the next questions: Start with an empty AVL tree and insert each of the given nodes in the order given. Rebalance after each insertion. You do not need to draw each insertion separately, but you must draw the tree immediately before every rotation and say what the rotations are.

3. 1, 2, 3, 5, 4

   Inserting 1,2,3

   

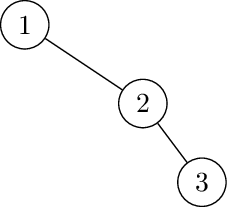
   Left rotate at 1: insert 5 4

   

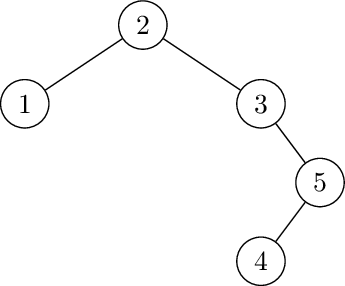
   Left-Right rotate at 3. First left rotate at 4

   

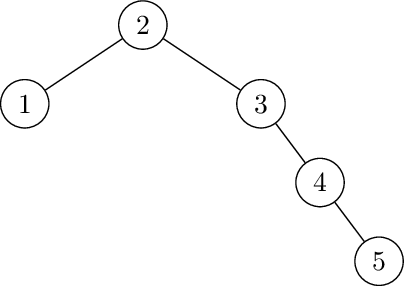
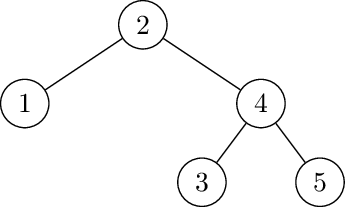
   Then right rotate at 3:

   

4. 15, 3, 9, 8, 14, 13, 12, 11, 10

   Inserting 15,3,9

   

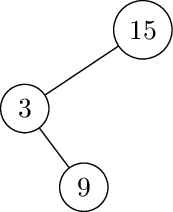
   Left-Right rotate at 15: Left rotate at 3.

   

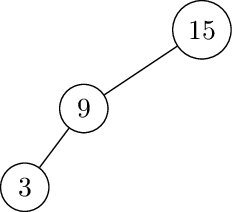
   Then, right rotate at 15. Insert 8, 14, 13.

   

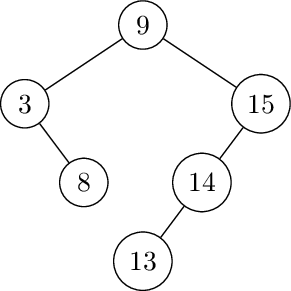
   Left rotate at 15. Insert 12, 11.

   

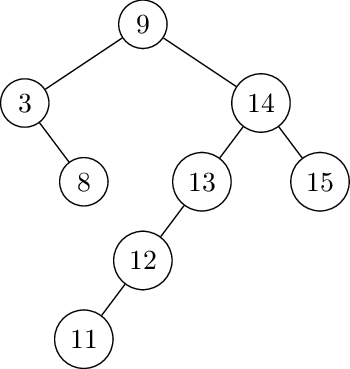
   Right rotate at 13. Insert 10.

   

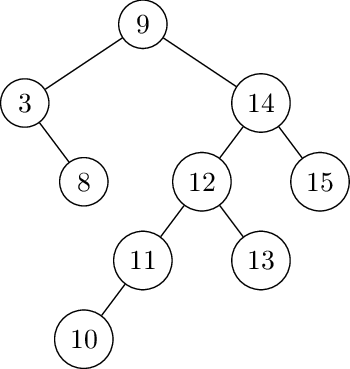
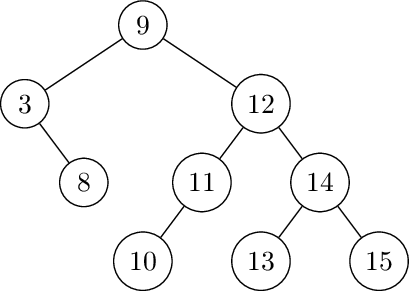
   Left rotate at 14

   

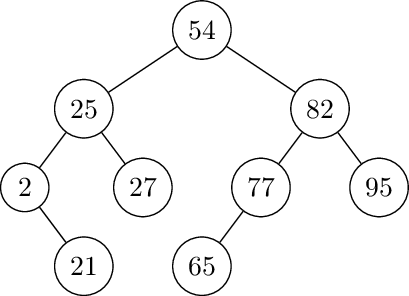
5. 77, 82, 2, 25, 54, 27, 21, 95, 65

   Insert 77, 82, 2, 25, 54.

   

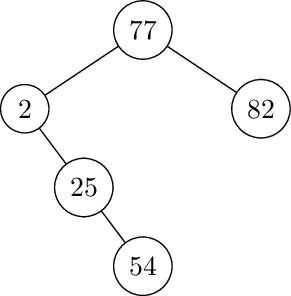
   Left rotate at 2. Insert 27.

   

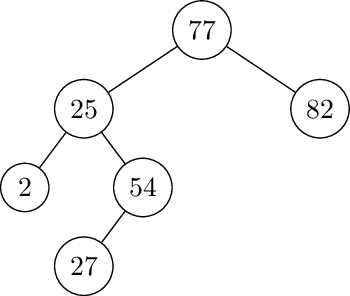
   Left-Right rotate at 77. First left rotate at 25

   

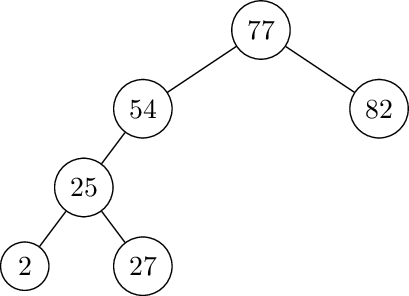
   Right rotate at 77. Insert 82, 95.

   

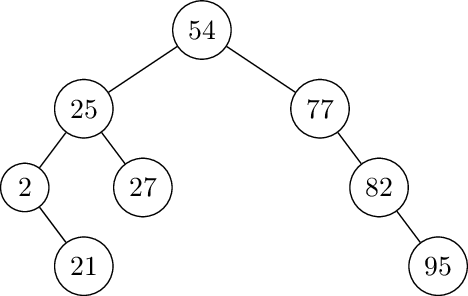
   Left rotate at 77. Insert 65

   

For the next two problems, starting with an empty 2-3-4 tree, insert each of the given letters into the tree, in the order given. Show your work, and clearly indicate the final state of the 2-3-4 tree after all the insertions.

6. F L A M E T H R O W I N G

   Insert F L A

   

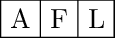
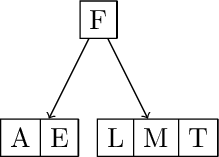
   Split and promote F. Insert M E T

   

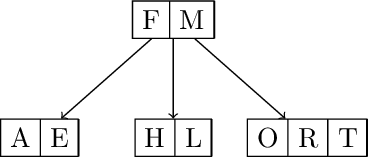
   Spit and promote M. Insert H R O

   

   Split and promote R. Insert W I N

   

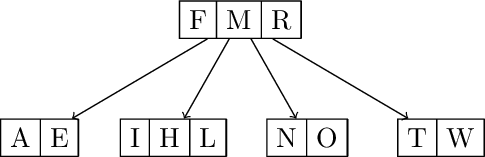
   Split and promote M

   

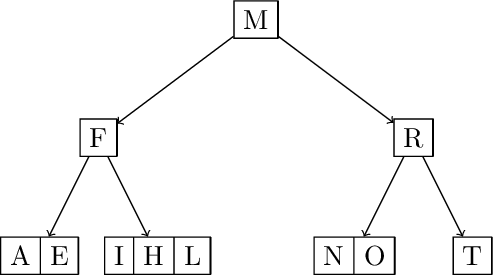
   Split and promote H. Insert G

   

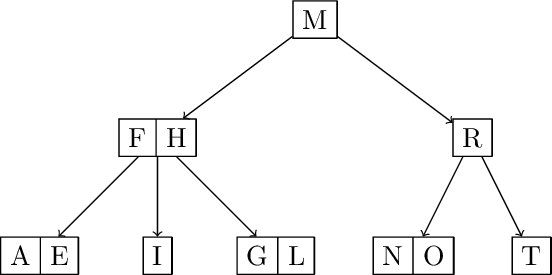
7. T A N K F U L S Z E R O

   Insert T A N

   

   Split and promote N. Insert K F U

   

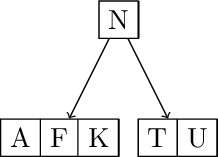
   Split and promote F. Insert L S

   

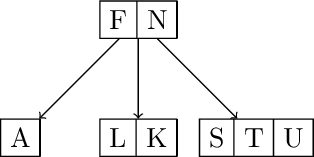
   Split and promote T. Insert Z E R O

   

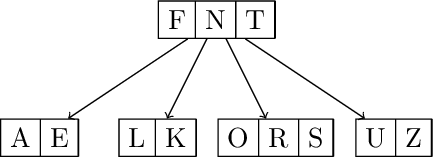
8. L U M B E R J A C K

   Insert L U M

   

   Split and promote M. Insert B E R

   

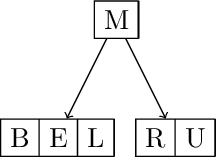
   Split and promote E. Insert J A C K

For the next two problems, I mostly need the final answer, but you need to show your work That might mean showing the series of trees that you made to find the answer, or explaining how else you figured it out. Of course, you should clearly indicate your final answer.

9. Starting with an empty 2-3-4 tree, and inserting the letters of the alphabet A, B, C, D, … in order, the first time the tree would grow to height 1 would be after inserting D. After inserting what letter would the tree grow to height 2 for the first time?

   Solution: The tree height increase will occur when ever all the nodes along the right most path are 4-nodes (or store 3 key/values). Because we are inserting in order, the remaining nodes must be 2-nodes (or store 1 key-value pair). Given that, the next time we'll split the root node is when there are three 2-nodes and two 4-nodes, or 3*1 + 3*2 = 9 inserts to reach that state, plus 1 to cause the splitting. The 10'th letter of the alphabet is J.

   This is visualized below:

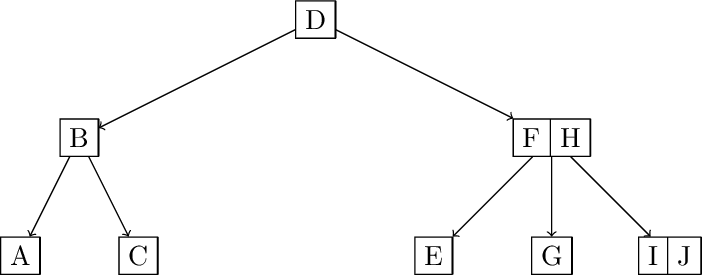
   Insert from A-I:

   

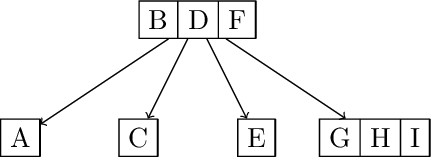
   Inserting J:

   

10. Now answer the same question, but for height 3. So, starting with an empty tree and inserting A, B, C, … in order, after inserting what letter would the tree grow to height 3 for the first time?

    Solution: Using similar logic, this time the next time the tree will grow is when there are three 4-nodes, and all remaining nodes are 2-nodes. That means that there are three subtrees of height 1 made entirely of 2-nodes (a binary tree) and three additional 2-nodes in the right most path. That is a total of 12 2-nodes and three 4-nodes: 12*1 + 3*3 = 21 so the 22'nd insert causes the height to grow. V is the 22'nd letter in the alphabet.

    Insert from A-U:

    

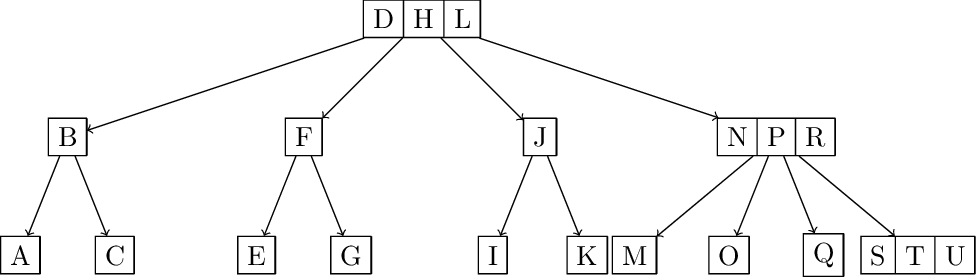
    Inserting V:

    

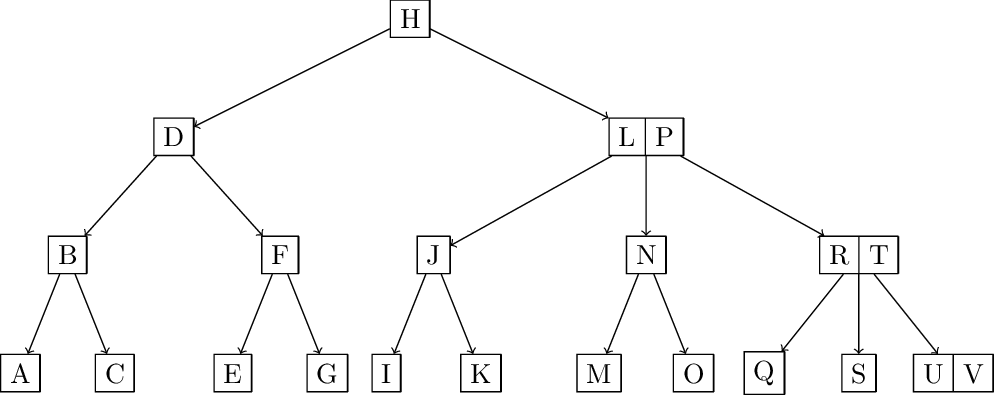
Bonus Problem (+5 points) Come up with an exact formula for the maximum number of nodes in a 2-3-4 tree of any height \(h\), if insertions are performed the way we did it in class.

Solution: Note that the branching factor is 4 for a maximally filled 2-3-4 tree. So level 0 of a tree stores 1 node, level 2 stores 4 nodes, level 3 stores 16 nodes, and so on. This leaves us with the following formula and solving using the geometric:

\[ \sum_{i=0}^{h} 4^i = \frac{1-4^{h+1}}{1-4} = \cfrac{1}{3}(4^{h+1}-1) \]